WSZYSTKO O LICZBACH

ZBIORY LICZBOWE

Zbiór liczbowy to zbiór, którego elementami są liczby.

ZBIÓR LICZB NATURALNYCH N
N = {0, 1, 2, 3,... }
W zbiorze liczb naturalnych najmniejszą liczbą jest 0. Następne liczby powstają przez dodanie 1 do poprzedniej.
W zbiorze liczb naturalnych nie ma liczby największej - zbiór jest nieskończony.

ZBIÓR LICZB CAŁKOWITYCH Z (często oznacza się liczby całkowite literą C)
Z = { ..., -3, -2, -1, 0, 1, 2, 3, ...}
Liczby całkowite to liczby naturalne i do nich przeciwne.
Zbiór liczb całkowitych jest zbiorem nieskończonym - nie ma elementu najmniejszego, ani największego.

ZBIÓR LICZB WYMIERNYCH Q (zbiór liczb wymiernych oznacza się również literą W)
Każdą liczbę wymierną można przedstawić w postaci ułamka dziesietnego skończonego lub rozwinięcia dziesiętnego nieskończonego okresowego:
, gdzie p jest liczbą całkowitą, q liczbą całkowitą różną od zera.
Rozwinięcie dziesietne liczby, otrzymuje się przez podzielenie p przez q, np.:
- rozwinięcie dziesiętne skończone

- rozwinięcie dziesiętne nieskończone, okresowe (liczba 6 jest okresem rozwinięcia)

ZAMIANA UŁAMKA DZIESIĘTNEGO NIESKOŃCZONEGO OKRESOWEGO NA UŁAMEK ZWYKŁY
Przykład:
Mamy przedstawić ułamek 0, 33333... = 0,(3), w postaci ułamka zwykłego.
Przyjmijmy: a = 0,3333... i pomnóżmy obie strony równania przez 10 (okresem ułamka jest jedna liczba - 3).
Otrzymamy: 10a = 3,333..., a więc 10a = 3 + 0,333..., czyli 10a = 3 + a.
Obliczamy a z danego równania: 10a - a = 3, to 9a = 3
Ostatecznie mamy:
Jeżeli okresem ułamka będą 2 liczby, np.; 0,2727... = 0,27, postępujemy bardzo podobnie jak w powyższym przykładzie, jedynie obie strony równania będziemy mnożyć przez 100:
a = 0,2727..., a więc po pomnożeniu przez 100, otrzymujemy: 100a = 27, 27...
czyli 100a = 27 + 0,27...
100a = 27 + a. Wyznaczając a z równania otrzymujemy:
W przypadku kiedy okresem ułamka będą 3, 4, ... itd. liczby, postępujemy podobnie, mnożąc obie strony równania odpowiednio przez 1000, 10000, ...itd

ZBIÓR LICZB NIEWYMIERNYCH NW
liczbą niewymierną nazywamy tę liczbę, która nie jest liczbą wymierną, a więc nie da się przedstawić w postaci ilorazu liczb p i q.
Rozwinięcie dziesiętne liczby niewymiernej jest nieskończone i nieokresowe.
Do liczb niewymiernych zaliczamy np.: , liczbę pi

ZBIÓR LICZB RZECZYWISTYCH R
Zbiór liczb rzeczywistych to zbiór liczb, które możemy zapisać za pomocą rozwinięcia dziesiętnego skończonego lub nieskończonego.
Do zbioru liczb rzeczywistych zaliczamy wszystkie omówione wcześniej zbiory liczb, a więc zbiór liczb: naturalnych, całkowitych, wymiernych i niewymiernych - są one podzbiorami zbioru R.

DO GÓRY

PRZEDZIAŁY LICZBOWE

PRZEDZIAŁY OGRANICZONE
przedział otwarty (a,b) - do przedziału należą wszystkie liczby leżąca na osi liczbowej między liczbami a i b, bez tych liczb.

przedział obustronnie domknięty [a,b] - do przedziału należą wszystkie liczby leżąca na osi liczbowej między liczbami a i b, włącznie z tymi liczbami: .

przedział lewostronnie domknięty [a,b) - do przedziału należą wszystkie liczby leżąca na osi liczbowej między liczbami a i b, włącznie z liczbą a, bez liczby b: .

przedział prawostronnie domknięty (a,b] - do przedziału należą wszystkie liczby leżąca na osi liczbowej między liczbami a i b, włącznie z liczbą b, bez liczby a: .

PRZEDZIAŁY NIEOGRANICZONE

Przedział lewostronnie otwarty i prawostronnie nieograniczony	Przedział prawostronnie otwarty i lewostronnie nieograniczony
Przedział lewostronnie domknięty i prawostronnie nieograniczony	Przedział prawostronnie domknięty i lewostronnie nieograniczony

DO GÓRY

DZIAŁANIA I PRAWA DZIAŁAŃ

DO GÓRY

CECHY PODZIELNOŚCI LICZB

LICZBY PIERWSZE - to takie liczby naturalne, które mają tylko dwa dzielniki: 1 i samą siebie.

LICZBY ZŁOŻONE - to takie liczby naturalne, które mają więcej niż dwa dzielniki.

NAJWIĘKSZY WSPÓLNY DZIELNIK pary liczb naturalnych a i b - NWD(a,b), to największa liczba naturalna przez którą dzieli się bez reszty zarówno a jak i b.

NAJMNIEJSZA WSPÓLNA WIELOKROTNOŚĆ pary liczb naturalnych a i b - NWW(a,b), to najmniejsza liczbę naturalna przez którą dzieli się bez reszty zarówno a jak i b.

LICZBY WZGLĘDNIE PIERWSZE, to liczby naturalne, dla których największym wspólnym dzielnikiem jest liczba 1 (NWD(a,b)=1).

Liczba naturalna jest podzielna przez:

DO GÓRY

POTĘGI I PIERWIASTKI

POTĘGĄ liczby rzeczywistej o wykładniku naturalnym n (n większe lub równe 1) nazywamy iloczyn n jednakowych czynników:

Jeżeli a jest różne od zera i n = 0, to a⁰ = 1
Jeżeli a jest dowolną liczbą rzeczywistą i n = 1, to a¹ = a

aⁿ = b
gdzie: aⁿ - n-ta potęga liczby a (czytamy a do potęgi n)
n - wykładnik potęgi
a - podstawa potęgi
b - wartość potęgowania

Jeżeli wykładnik potęgi n = 2, to czytamy kwadrat liczby a, np.: 4² = 16 (kwadrat liczby 4 wynosi 16)
Jeżeli wykładnik potęgi n = 3, to czytamy sześcian liczby a, np.: 2³ = 8 (sześcian liczby 2 wynosi 8)

Działania na potęgach

Podstawy potęg a i b należą do zbioru liczb rzeczywistych, a wykładniki potęg m i n do zbioru liczb całkowitych

PIERWIASTKIEM stopnia n liczby nieujemnej a, nazywamy taką liczbę nieujemną b, która podniesiona do potęgi n daje a:

n - stopień pierwiastka
a - liczba podpierwiastkowa
b - pierwiastek n-tego stopnia z liczby a (wartość pierwiastkowania)

Nie określa się pierwiastków liczb ujemnych.

Przykład: , bo 4² = 16
, bo 5³ = 125

Działania na pierwiastkach

Liczby podpierwiastkowe a i b są dodatnie (mogą być 0), a stopnie m i n pierwiastka są liczbami naturalnymi oprócz 0 i 1.

DO GÓRY

PROCENTY

Jeden procent (1%) pewnej liczby a (lub innej wielkości), nazywamy setną część tej liczby (wielkości) i oznaczamy 1% a

Aby liczbę zamienić na procent, należy tę liczbę pomnożyć przez 100 i dopisać symbol %, np.:
0,25 . 100% = 25%
2 . 100% = 200%

Aby procent zamienić na liczbę, należy liczbę wyrażającą procent pomnożyć przez 0,01 (podzielić przez 100)np.:
12% = 12 : 100 = 0,12
250% = 250 : 100 = 2,5

Aby obliczyć procent danej liczby należy pomnożyć tę liczbę przez dany procent, np.:
5% liczby 300, to 5% . 300 = 0,05 . 300 = 15
25% liczby 1000, to 25% . 1000 = 0,25 . 1000 = 250

Aby obliczyć liczbę z danego jej procentu, należy podzielić tę liczbę przez dany procent. 5% pewnej liczby wynosi 40, to 40 : 5% = 40 : 0,05 = 800
20% pewnej liczby wynosi 6, to 6 : 20% = 6 : 0,20 = 30

Aby obliczyć jakim procentem jednej liczby jest druga liczba, należy drugą liczbę podzielić przez pierwszą i otrzymany iloraz wyrazić w procentach, np.:
Jakim procentem liczby 10 jest liczba 2? (2 : 10) . 100% = 20%
Jakim procentem liczby 200 jest liczba 4? (5 : 200) . 100% = 2%

OBLICZANIE ODSETEK

PROCENT SKŁADANY to sposób oprocentowania wkładu pieniężnego K, polegający na doliczaniu rocznego dochodu w postaci odsetek do wkładu, który procentuje wraz z wkładem w następnym roku.

gdzie: K - wysokość kredytu do spłaty
K_o - otrzymany kredyt
p - oprocentowanie
n - liczba lat spłaty
k - liczba kapitalizacji w roku

DO GÓRY

CIEKAWE LICZBY

Nazwa "ludolfina" pochodzi od imienia matematyka holenderskiego Ludolfa van Ceulena, który w 1610 roku obliczył wartość liczby pi z dokładnością do 35 cyfr po przecinku.
π = 3,1415926535897932384626433832795028
Symbol liczby po raz pierwszy został użyty w 1706 roku przez matematyka angielskiego Wiliama Jonesa, ale powszechnie zaczął być używany dopiero w połowie XVIII wieku po wydaniu przez L.Eulera "Analizy".
Pierwsze oszacowania liczby wprowadzili Babilończycy około 2000 p.n.e., przyjmując jej wartość równą 3.

Liczba π jest liczbą niewymierną, określającą stosunek długości okręgu do długości jego średnicy.

W celu zapamiętania pierwszych cyfr rozwinięcia dziesiętnego liczb, wystarczy poznać jeden z wielu powstałych wierszy. Licząc litery w poszczególnych wyrazach otrzymujemy kolejne cyfry π.
Najbardziej znany jest wiersz Kazimierza Cwojdzińskiego:

Kuć i orać w dzień zawzięcie,
bo plonów niema bez trudu.
Złocisty szczęścia okręcie kołyszesz...
Kuć. My nie czekajmy cudu.
Robota. To potęga ludu.

LICZBY DOSKONAŁE

Liczby doskonałe wprowadzili pitagorejczycy, podając pierwsze cztery kolejne: 6, 28, 496, 8128.
Liczba doskonała to taka liczba, która jest równa sumie wszystkich swoich dzielników mniejszych od niej samej np.: 6=1+2+3, 28=1+2+4+7+14.
Do dziś znaleziono tylko 39 liczb doskonałych. Odkryte dotychczas wszystkie liczby doskonałe są parzyste, nie znaleziono liczby nieparzystej.
Regułę znajdowania liczb doskonałych parzystych podał Euklides już w IV w. p.n.e., a potwierdził ją 2000 lat później Leonhard Euler:
N=2^k-1(2^k-1)
gdzie 2^k-1 musi być liczbą pierwszą dla k>1 (naturalnego).
Ostatnią liczbę doskonałą znaleziono w 2001 roku.
Największą odkryta dotychczas liczba doskonała ma postać: 2^13466916 * (2^13466917 - 1).

"ZŁOTA" LICZBA

Wyraża ona długość odcinka spełniającego warunek tzw. złotego podziału.
Złoty podział to taki podział odcinka na dwie części, aby stosunek długości dłuższej z nich do krótszej był taki sam, jak całego odcinka do części dłuższej

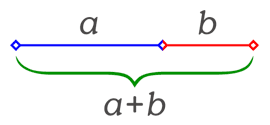
(a+b) : a = a : b

Złoty podział można znaleźć przykładowo w pięciokącie foremnym: jest to punkt przecięcia jego przekątnych.
Liczba złota ma ciekawe własności:
- aby ją podnieść do kwadratu, wystarczy dodać do niej jedynkę,
- aby znaleźć jej odwrotność, wystarczy odjąć jedynkę.
W starożytności przypisywano złotemu podziałowi odcinka wyjątkowe walory estetyczne i używano go jako miary proporcji w architekturze.
Czy wiesz, że...
złoty podział - to wymiary znormalizowanego zeszytu, które pozostają w stosunku równym stosunkowi złotego podziału.

LICZBY ZAPRZYJAŹNIONE

liczby naturalne m i n, spełniające warunek: suma wszystkich mniejszych od m dzielników naturalnych liczby m równa się n i jednocześnie suma wszystkich mniejszych od n dzielników naturalnych liczby n jest równa m.
Przykładem liczb zaprzyjaźnionych jest para 220 i 284.
m = 220 n = 284
suma wszystkich mniejszych dzielników liczby m, wynosi:
1 + 2 + 4 + 5 + 10 + 11 + 20 + 22 + 44 + 55 + 110 = 284 = n
suma wszystkich mniejszych dzielników liczby n, wynosi:
1 + 2 + 4 + 71 + 142 = 220 = m
Każda liczba doskonała jest zaprzyjaźniona sama ze sobą.
Obecnie znanych jest około dwóch milionów par liczb zaprzyjaźnionych.
Liczby zaprzyjaźnione znali już pitagorejczycy i przypisywali im znaczenie mistyczne.
Nazwę liczb przypisuje się Pitagorasowi, którego gdy zapytano: "Co to jest przyjaciel?" - odpowiedział:
"Przyjaciel to drugi ja; przyjaźń, to stosunek liczb 220 i 284".

LICZBY BLIŹNIACZE

Dwie liczby pierwsze, których różnica wynosi 2, to liczby bliźniacze.
Przykładami par liczb bliźniaczych są: 3 i 5, 5 i 7, 11 i 13, 17 i 19.

LICZBY PALINDROMICZNE

Liczbę naturalną, którą czyta się tak samo od początku i od końca nazywamy palindromem.
Przykłady liczb palindromicznych: 66, 323, 494, 30703, 5139315...

LICZBY LUSTRZANE

To takie dwie liczby, które są lustrzanym odbiciem, np.: 98 i 89, 123 i 321, 1245 i 5421...
Jeżeli napiszemy dowolną liczbę i jej lustrzane odbicie, to tak otrzymana liczba jest podzielna przez 11, np.: liczba 12 i 21 to 1221 : 11 = 192.

DO GÓRY